koordinatni sustav

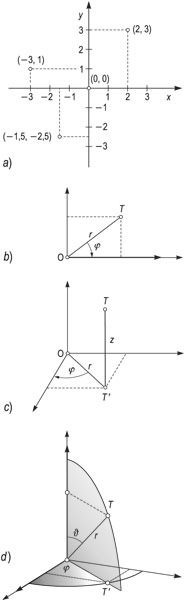
koordinatni sustav (engl. coordinate system; njem. Koordinatensystem; rus. система координат), geometrijski sustav u kojem se nekoj točki na pravcu, u ravnini ili u prostoru dodjeljuje uređeni skup realnih brojeva i tako jednoznačno određuje njezin položaj. Ti se brojevi nazivaju  → koordinatama. Koordinatni sustav na pravcu brojevni je pravac (jedna koordinatna os), a položaj točke određen je realnim brojem (jedna koordinata). Kartezijev ravninski pravokutni koordinatni sustav određuju dva međusobno okomita pravca, tj. dvije koordinatne osi (os apscisa i os ordinata), a koordinate su x (apscisa) i y (ordinata). Sjecište koordinatnih osi jest ishodište O koordinatnoga sustava, s koordinatama (0, 0). Položaj točke određuje uređen par realnih brojeva (x, y), tj. koordinate okomitih projekcija točke na os apscisa i na os ordinata. Koordinate su desno i gore od ishodišta pozitivne, a lijevo i dolje negativne. Ravninski polarni koordinatni sustav određuje zraka (polarna os) s početkom u ishodištu. Položaj točke T određuje uređen par realnih brojeva (r, φ), tj. udaljenost točke od ishodišta r i kut φ što ga polarna os zatvara s dužinom OT. Kartezijev prostorni pravokutni koordinatni sustav određuju tri međusobno okomita pravca, tj. tri koordinatne osi (os apscisa, os ordinata i os aplikata), s koordinatama x (apscisa), y (ordinata) i z (aplikata), koje se sijeku u ishodištu s kordinatama (0, 0, 0). Položaj točke određuje uređena trojka realnih brojeva (x, y, z), tj. udaljenosti okomitih projekcija točke na apscisu, ordinatu i aplikatu od ishodišta. Kartezijev prostorni kosokutni koordinatni sustav određuju pravci koji nisu međusobno okomiti, a projekcije točke na koordinatne osi su kose. Primjenjuje se npr. u teoriji kristala. Prostorni cilindrični koordinatni sustav određuju tri međusobno okomita pravca x, y, z. Položaj točke određuje uređena trojka realnih brojeva (r, φ, z), gdje je r udaljenost projekcije T' točke T na ravninu xy od ishodišta, φ je kut što ga dužina OT' zatvara s polarnom osi, z je udaljenost od ishodišta okomite projekcije točke T na os aplikata. Prostorni sferni koordinatni sustav određuju tri međusobno okomita pravca x, y, z. Položaj točke određuje uređena trojka realnih brojeva (r, ϑ, φ), gdje je r udaljenost točke T od ishodišta, ϑ kut što ga dužina OT zatvara s osi z, a φ kut što ga projekcija OT' dužine OT na ravninu xy zatvara s osi x. Sferni pravokutni koordinatni sustav određuju dvije kružnice: apscisna kružnica koja je ishodišni (nulti, polazni) meridijan, te ordinatna kružnica koja je najveća kružnica sfere okomita na meridijan. Položaj točke određuju dvije koordinate (x, y): prva je udaljenost projekcije točke na ordinatnu kružnicu, mjerena uzduž meridijana, a druga je duljina luka kružnice okomite na meridijan, mjerena od ishodišnoga meridijana do te točke. Primjenjuje se u geodeziji i geografiji. Horizontski koordinatni sustav određuju dvije kružnice: horizont i na horizont okomita kružnica, koja prolazi kroz zenit. Položaj točke na nebu određuje uređeni par brojeva, koordinate (α, h): prva je azimut α, kut na kružnici u ravnini horizonta mjeren od juga u smjeru kazaljke na satu do okomite projekcije točke na horizont, a druga je visina h, kut na kružnici okomitoj na horizont, mjeren od horizonta do točke. Primjenjuje se u astronomiji i navigaciji.