vektorska algebra

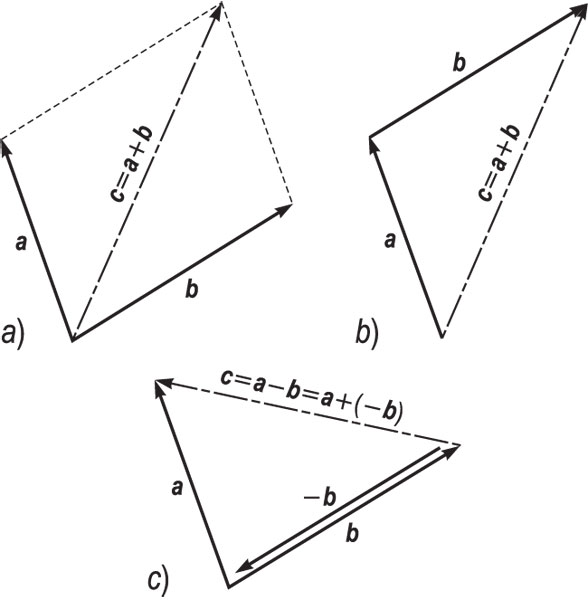
vektorska algebra (engl. vector algebra; njem. Vektoralgebra; rus. векторная алгебра), grana algebre koja se bavi operacijama na vektorima, tj. njihovim zbrajanjem, množenjem sa skalarima i međusobnim skalarnim i vektorskim množenjem vektora. Vektori se zbrajaju tako da se zbroje pojedine projekcije na osima, npr. a + b = (a_x + b_x) i + (a_y + b_y) · j + (a_z + b_z) · k, ili grafičkim postupkom, tzv. pravilom trokuta ili pravilom višekuta. Skalarom se → vektor množi tako da se svaka komponenta množi skalarom, npr. λ · a = λ · a_x · i + λ · a_y · j + λ · a_z · k. Vektori se međusobno množe na dva načina. Skalarnim umnoškom naziva se umnožak vrijednosti vektora koji ima svojstva komutativnosti, asocijativnosti i distributivnosti, a rezultat → množenja je skalar. Označuje se točkom u sredini retka, npr. a · b = b · a = a_x · b_x + a_y· b_y + a_z · b_z = a · b cos φ, gdje je φ kut između vektora. Vektorski umnožak ima svojstva antikomutativnosti, neasocijativnosti i distributivnosti, a rezultat je množenja vektor. Označuje se nagnutim križićem (×), npr.:

\[{\pmb a}\times{\pmb b}=-\,{\pmb b}\times{\pmb a}=\left|\matrix {{\pmb i}&{\pmb j}&{\pmb k}\cr a_x&a_y&a_z\cr b_x&b_y&b_z}\right|=\]

= i · (a_y · b_z – b_y · a_z) + j · (a_z · b_x – b_z · a_x) + k · (a_x · b_y – b_x · a_y).